library(lavaan) # install.packages("lavaan")
library(tidyverse) # install.packages("tidyverse")
library(rio) # install.packages("rio")
library(psych) # install.packages("psych")
library(combinat) # install.packages("combinat")
library(devtools) # install.packages("devtools")
library(sleasy) # devtools::install_github("JoranTiU/sleasy")21 Structural Equation Modeling with R for Education Scientists
Abstract
Structural Equation Modeling (SEM) is a method for modeling the multitude of relationships between latent variables and the observable indicators, as well as the relationship between the latent variables themselves to test theories. In its most common form, SEM combines confirmatory factor analysis (CFA with another method named path analysis. Just like CFA, SEM relates observed variables to latent variables that are measured by those observed variables and, as path analysis does, SEM allows for a wide range of regression-type relations between sets of variables (both latent and observed). This chapter presents an introduction to SEM, an integrated strategy for conducting SEM analysis that is well-suited for educational sciences, and a tutorial on how to carry out an SEM analysis in R.
1 Introduction
Educational research involves a variety of theoretical constructs that are not directly observable (e.g., motivation, engagement, cognitive development, and self-regulation) and that can only be indirectly studied by looking at participant’s responses to observable indicators of these constructs (e.g., participants’ responses to questionnaire items). The previous chapter about factor analysis [1] showed how to assess the factor structure of these unobserved, or latent, constructs and, thus, which items are good measurements of these constructs. This is crucial for developing valid instruments to measure (i.e., quantify) the latent constructs encountered in educational research. However, good measurement of latent constructs is typically not the researchers' ultimate goal. Usually, they subsequently want to answer questions about relationships or mean differences between (multiple) of these constructs, such as, “Is teacher motivation related to student engagement?” or “Does student engagement significantly differ for small and large-scale teaching styles?” If researchers only have (i) observed variables (e.g., years of teacher experience) for both predictor and outcome variables and (ii) want to investigate the effect of one or more predictor variables on a single outcome variable at a time (e.g., the effect of teacher experience and teacher gender on student GPA), these types of questions can be answered using familiar analysis methods such as multiple regression or ANOVA. However, as soon as questions involve latent variables or testing an entire system of (complex) interrelations between variables (like the ones found in most theoretical frameworks), researchers need an analysis technique with more flexibility that allows for modeling a multitude of relationships between (latent and/or observed) variables simultaneously [2]; that is, researchers need SEM.
At its core, SEM is a mix of factor analysis (discussed in the previous chapter) and a method called path analysis, which was invented by Wright [3]. One can think of path analysis as a type of multiple regression analysis because it also allows estimating and testing direct effects between variables. However, while multiple regression merely allows for testing the direct effects of predictor(s) on only a single outcome variable, path analysis can look at both direct and indirect effects between whole sets of predictor(s) on whole sets of other variables simultaneously. This implies that in path analysis, a variable can simultaneously be an outcome and a predictor: a variable might be predicted by one or more variables while also serving as a predictor for other variables. In other words, with path analysis, researchers can pretty much fit any model they can dream of as long as all variables are observed. Fitting a path model to latent variables requires going beyond path analysis. Fortunately, Jöreskog and Van Thillo [4] developed a statistical software called LISREL that allowed the use of latent variables in path analysis and thereby created SEM. Over the years, their work has been integrated into increasingly user-friendly software, contributing to the widespread use of the technique in social sciences today. This widespread use has also led to the definition of a SEM model becoming less concrete as the term is now also used for models with only observed variables, even though that would officially be a path model.
2 Literature review
Perhaps the most well-known application of SEM in education research is the technology acceptance model (TAM), used to explain teachers’ adoption of education technology [5]. The model hypothesizes that a teacher's decision to adopt and use technology is influenced by their perceptions of its ease of use and usefulness. These perceptions shape their attitude toward technology use, which, in turn, affects their intention to use it and their actual usage. Such complex interplay in factors that influence technology acceptance requires using sophisticated methods such as SEM. The model has been extensively applied and validated in several contexts [6], investigating the adoption of multiple technological innovations such as serious games [7], virtual reality [8], or artificial intelligence [9]. The model has also been extended in several ways throughout the years to address the influence of other factors such as personality traits, result demonstrability, and risk, among many others [10].
Many other applications of SEM exist in education research. For example Kusurkar et al. [11] used SEM to investigate how motivation affects academic performance. They hypothesized that greater levels of self-determined motivation are associated with the adoption of effective study strategies and increased study dedication, resulting in improved academic achievement. Their findings confirmed that the influence of motivation on academic performance is mediated by the use of effective study strategies. The work by Kucuk and Richardson [12] examined the interconnections between the three types of Community of Inquiry presence (teaching, social, and cognitive), four engagement components (agentic, behavioral, cognitive, and emotional), and satisfaction in online courses. The findings suggest that teaching presence, cognitive presence, emotional engagement, behavioral engagement, and cognitive engagement were significant predictors of satisfaction, explaining 88% of its variance.
The rise of digital learning and the opportunities for unobtrusive data collection have given rise to a new wave of studies that take advantage of the trace log data that students leave behind in online systems [13], instead of relying on self-reported data from questionnaires. For instance, Koç [14] proposed a model that explains the association between student participation and academic achievement. Student participation was measured through attendance to online lectures and discussion forum submissions. His results suggest that “student success in online learning [can] be promoted by increasing student participation in discussion forums and online lectures with more engaging learning activities” [14]. Fincham et al. [15] validated a theorized model of engagement in learning analytics using factor analysis and SEM. He found that affective engagement (measured by sentiment, sadness, and joy of students’ writing) and cognitive engagement (measured by syntactic simplicity, word concreteness, and referential cohesion) are not significantly associated with students’ final grades but academic and behavioral engagement (problem submissions, videos watched, and weeks active) are.
The rest of this chapter presents a recap of SEM, an integrated strategy for conducting a SEM analysis that is well suited for Educational Sciences, and an illustration of how to carry out a SEM analysis in R. Like the previous chapter, the presentation in this chapter will be kept applied and focus on how to conduct the analysis in R, instead of diving into technical details (for this, interested readers are referred to the readings listed at the end of this chapter).
3 Recap of SEM
In its most common form, SEM combines confirmatory factor analysis (CFA) with path analysis. Like CFA, SEM relates observed variables to latent variables that are measured by those observed variables, and, like path analysis, SEM allows for a wide range of relations between entire sets of variables (both latent and observed). As mentioned before, SEM is nowadays an umbrella term that also includes path analysis with only observed variables. However, this chapter focuses on SEM with latent variables to show its full potential. For the sake of brevity, it is assumed that the readers of this chapter have already read the factor analysis chapter, where a good description and recap of CFA (and how it differs from exploratory factor analysis) is provided.
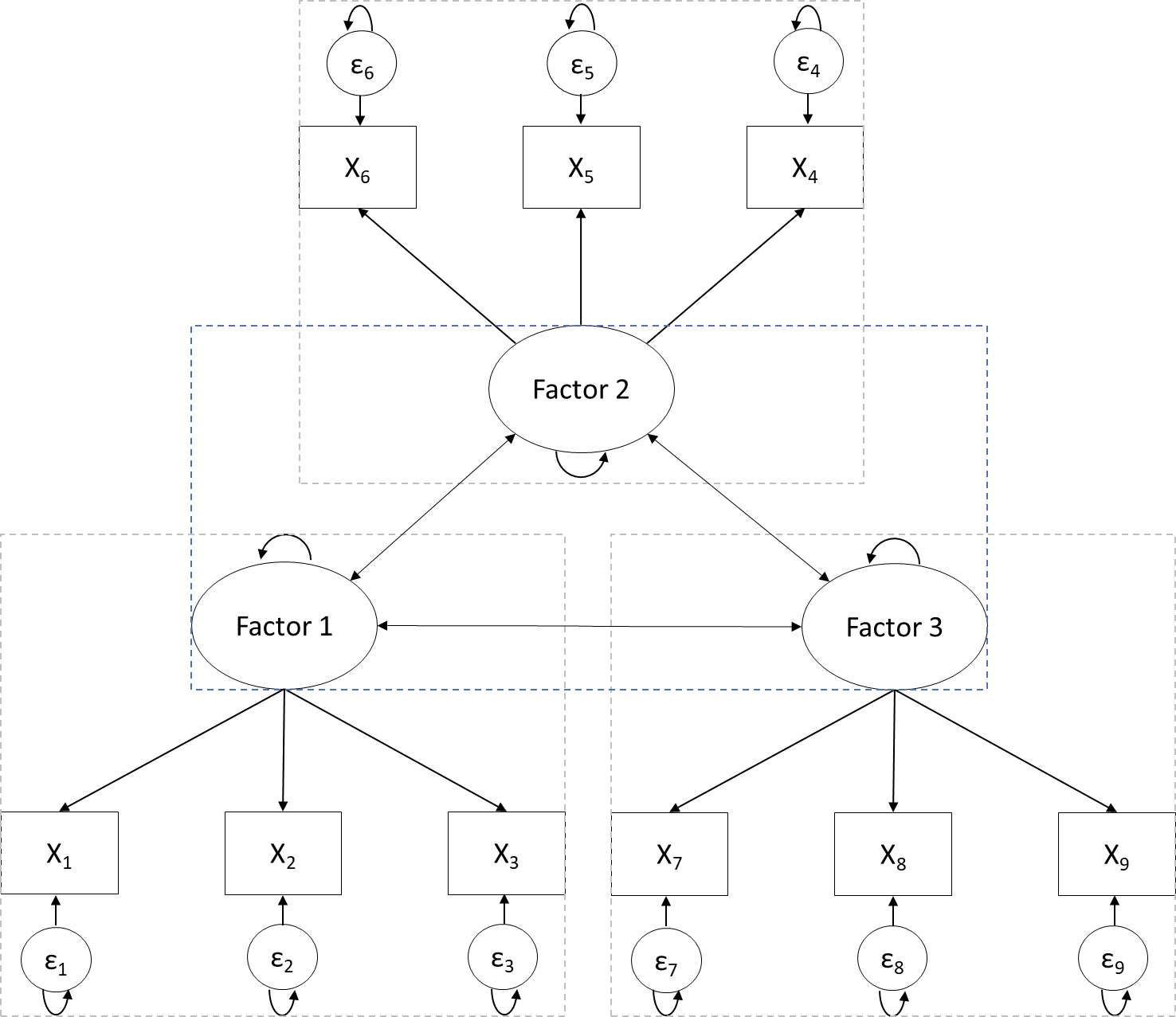
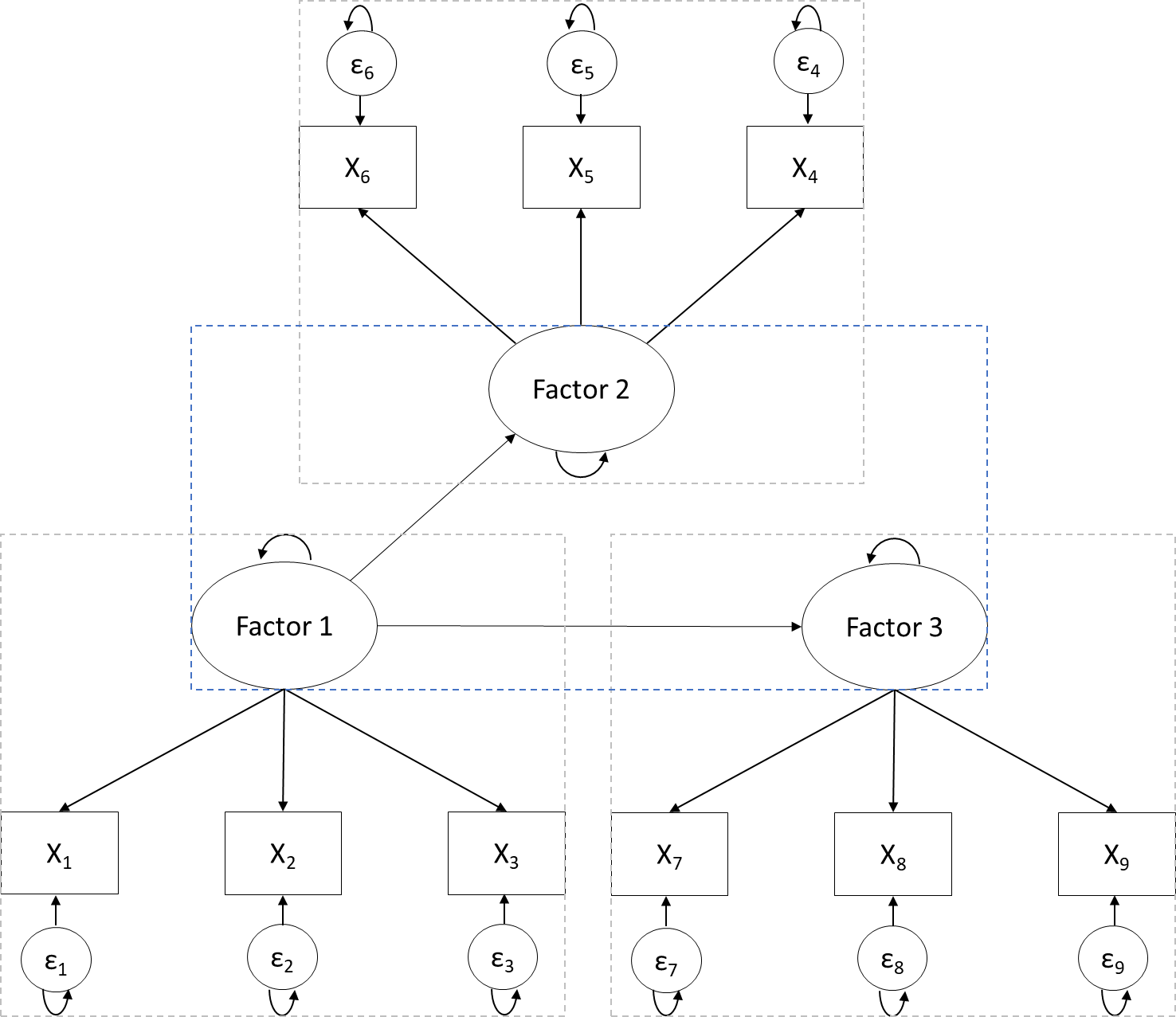
The similarity between CFA and SEM is illustrated in Figure 1. It can be seen that both models consist of a part in which the observed and latent variables are related to each other (these relations are referred to as the measurement model) and a part in which the latent factors are related to each other (these relations are referred to as the structural model). The crucial difference between CFA and SEM is that factors in CFA can only correlate with each other (see Figure 1a). In contrast, SEM gives us more flexibility regarding (the set of) relationships between (observed and latent) variables. For example, Figure 1b shows the same factor model as Figure 1a. However, in Figure 1b, Factors 2 and 3 are both predicted by Factor 1a but are unrelated beyond that. Which model researchers specify, that is, what relations between (latent) variables they model, is entirely up to them. However, this flexibility is also a danger of SEM: the fact that researchers can fit any model they can think of does not mean they should. Ideally, the chosen relationships are driven by theory and substantive knowledge of the field.
4 Integrated Strategy for Structural Equation Modeling
In the following, we guide you, the researcher, through the different steps of conducting a SEM analysis. It is important to highlight that the most crucial part of a SEM analysis is checking its assumptions and checking measurement invariance (which was already briefly mentioned in the previous chapter). Measurement invariance means that the factor model underlying your instrument apply equally to relevant subgroups in your sample. In other words, measurement invariance implies that if you analyzed each of those subgroups with factor analysis separately (using the three steps described in the previous chapter), you would find the same model in each one. Measurement invariance is crucial: As discussed in the previous chapter, the interpretation of a latent variable depends on the factor model. Therefore, if the factor model of the latent variable(s) in your SEM model differs, for example, across biological sex, you effectively throw apples and oranges together if you analyze both males and females simultaneously in your analysis, which will result in uninterpretable outcomes. At the very least, you would want the same factor model for everyone in terms of the same number of factors and the same pattern of relationships between the factors and the observed variables. This scenario is called configural invariance. However, most research questions require higher levels of invariance, in which not only the number of factors and the pattern of factor loadings are the same across subgroups, but also the actual values of (most of the) parameters such as factor loadings and intercepts are equal across groups. More information about the different levels of invariance and how and when to test for it is presented below. After you have checked the assumptions and measurement invariance, you can safely apply and interpret a SEM analysis. The actual SEM analysis is just the final step of the modeling strategy presented here.
4.1 Step 1: Steps from the previous chapter while assessing configural invariance
Since SEM analyses typically look at the relationship of one or more latent variables with one or more other (latent or observed) variables, you first need to ensure that the latent variables represent what you think they represent. To this end, the first step is going through some or all the steps described in the previous chapter for every latent variable you include. If you use a new instrument to measure the latent variables, you should go through all the steps from (1) exploring the data structure, (2) building the factor model and assessing fit, and (3) assessing generalizability1. As explained in the previous chapter, step 3 should be conducted using a holdout sample or a new sample. However, you can use the same (holdout or new) sample for your SEM analysis. More on determining sufficient sample sizes is discussed below in the “SEM in R” section.
Once the factor model of your latent variables has been established or verified, you must ensure that this structure applies to all relevant subgroups in your sample. That is, you need to check for measurement invariance. The first level of invariance is configural invariance and, thus, whether the number of underlying factors and the pattern of relations between those factors and the observed variables is the same in each relevant subgroup. To test for configural invariance, you must go through the steps outlined in the previous chapter for each relevant group in your sample separately. Note that this also means you need sufficient observations for model building and generalizability in each subgroup you want to consider. Which subgroups are important to consider separately will always come down to theory.
If you use an existing instrument on a sample from a population for which the instrument had already been validated and configural invariance attained in previous research (i.e., you have strong a priori assumptions about the CFA model), you could skip the three steps from the factor analysis chapter and go straight to assessing the fit of the CFA model to your data. If it fits, you can continue with the SEM analysis. However, even when using existing validated instruments, it is strongly recommended to follow all the aforementioned steps for each relevant subgroup of your sample, as your sample might differ in important ways from the ones on which the instrument was validated, which could potentially introduce biases into your results.
4.2 Step 2: Assessing Higher Levels of Invariance
After establishing configural invariance between relevant groups, it is time to verify that the factor model parameters (specifically the loadings and intercepts) are also invariant across the factor models of each group. To illustrate why these “higher levels of invariance” are important, assume you want to investigate the relationship between children’s age and how engaged they are in class. You measure the latent variable “classroom engagement” using a factor model on the three observed variables engages in group activities, asks for assistance when needed, and prefers working alone. Of these three variables, asks for assistance might be more indicative of classroom engagement for girls than for boys due to cultural stereotypes. Boys could be way less likely to ask for assistance, not because they are less engaged, but because society taught them that boys should not ask for help and should instead figure things out themselves. In this example, the interpretation of the latent variable would be different between girls and boys: for girls, you truly measure classroom engagement; for boys, you measure an uninterpretable mix of classroom engagement and how much they internalized gender stereotypes. If you ignored this between-group difference in the meaning of the latent variable when including it in a SEM model, you would come to invalid conclusions about the structural relationships between (latent or latent and observed) variables. Fortunately, the type of invariance in this example would show up as a difference in the relation between the factor classroom engagement and the variable asks for assistance between boys and girls. In other words, it would show up as a difference in factor loadings between groups.
Testing for higher levels of invariance in the factor model between categorical characteristics or “groups” (e.g., gender, nationality) can be done by testing for differences in model parameters between groups using a multi-group approach [16, 17] that compares the fit of a factor model in which all parameters are allowed to differ between groups to one in which one or more parameters are constrained to be equal across groups. If constraining parameters across groups does not cause a substantially worse model fit, invariance holds, and the constrained parameters can safely be considered and modeled as equal across groups. To assess for invariance across continuous variables (e.g., age) one could split the continuous variable into groups (e.g., changing the continuous variable age into the groups “young” and “old”), although one should ideally use more advanced methods like Moderated Non-Linear Factor Analysis [18] since categorizing continuous variables leads to loss of information. This chapter, however, will focus on the multi-group approach because it is the most common and widely available approach.
There are two important points about the invariance of model parameters that make the lives of researchers a little easier. First, not all model parameters have to be invariant. If you investigate relationships between (latent) constructs, as opposed to mean differences, only the factor loadings have to be invariant. For assessing differences in means, the factor loadings and the intercepts must be invariant. Note that the effects of categorical predictors on other variables also pertain to differences in means and that both loading- and intercept invariance are needed to interpret those effects. Note that a factor model comprises not only factor loadings and intercepts but also unique variances. However, unique variances do not have to be invariant across groups when looking at relationships or mean differences across latent variables. Therefore, we will not further consider them in this chapter. Second, the discussion of measurement invariance so far in this section has been about what is called full invariance, in which all parameters of a certain type (i.e., all factor loadings and/or all intercepts) are equivalent across groups (or across levels of a continuous variable). While this would represent an ideal situation, full invariance will rarely hold and is also not necessary. Partial invariance in which several, but not all, parameters of a certain type are invariant across groups is typically considered enough (e.g., the factor loadings of 4 out of 6 variables used to measure a factor are invariant across groups). Specifically, as long as at least two loadings are invariant across groups, one can look at relations between the corresponding latent variable and other (observed and/or latent) variables, and as long as at least two factor loadings and at least two intercepts are equal, one can meaningfully look at differences in means too ([19]; but also see [20]).
4.3 Step 3: Building the Structural Equation Model and Assessing Fit
After verifying the required level of measurement invariance for all latent variables that will be used in the SEM analysis, you are ready to investigate structural relations (e.g., regression relationships) between the factors (as well as observed variables if desired). Like with the factor models in the previous chapter, you first have to evaluate if the model fits your data sufficiently. You should only interpret the structural relations if the model fits the data. If the model does not fit, it is not a good description of the data and does not warrant further interpretation.
5 SEM in R
In the following, you will be taken through the essential steps of performing SEM in the open-source software R. To this end, the same dataset [21] will be used as the one to which factor analysis was applied to in the previous chapter [1]. The dataset contains survey data about teacher burnout in Indonesia. In total, 876 respondents have answered questions on five domains: Teacher Self-Concept (TSC, 5 questions), Teacher Efficacy (TE, 5 questions), Emotional Exhaustion (EE, 5 questions), Depersonalization (DP, 3 questions), and Reduced Personal Accomplishment (RPA, 7 questions). Thus, the total number of variables equals 25. The questions were assessed on a 5-point Likert scale (ranging from 1 = “never” to 5 = “always”). For more information on the dataset, the interested reader is referred to the data chapter of the book [22].
In line with the seven hypotheses about the structural relationships in the original article, the SEM analysis presented below tests whether TE is predicted by TSC and whether EE, DE, and RPA are respectively predicted by TE and TSC. Note that, as SEM builds up on factor analysis, the code presented below also builds up on the factor analysis results and syntax from the previous chapter. Without reading the previous chapter, the steps in this chapter might therefore be harder to follow.
To provide an example of how to assess between-group invariance of the constructs, it will be tested whether the same factor structure holds across gender. More specifically, because the running example is only interested in relationships between constructs and not mean differences, only loading invariance will be tested for. However, code to also test for intercept invariance will also be provided.
5.1 Preparation
To follow all the steps, you have to install the following packages with the function install.packages(). You only have to install them the first time you want to use them; therefore, the commands are commented below. Once you have the packages installed, you must load them with the library() function whenever you open the R script.
5.1.1 Reading in the data
The data can be read in, and the variable names can be extracted with the following commands:
dataset <- import("https://github.com/lamethods/data/raw/main/4_teachersBurnout/2.%20Response.xlsx")
var_names <- colnames(dataset)In the following, you will also find commands to add a gender variable to the dataset. This variable is only added to demonstrate how to perform invariance tests. Although the original data contains gender, it is unfortunately not part of the publicly shared data.2 The proportion of men (gender = 0) and women (gender = 1) in the created variable aligns with the reported values from the article corresponding to the dataset.
set.seed(1611)
dataset$gender <- as.factor((sample(c(rep(0, 618), rep(1, 258)))))5.1.2 Are the data suited for SEM?
Several data characteristics are necessary for SEM. These largely overlap with the necessary data characteristics for factor analysis, as discussed in the previous chapter (i.e., are the variables continuous? Are the correlations between the variables sufficiently large? Is there enough common variance among the variables? Are the data normally distributed?). Therefore, the steps in R to check whether the data are suited will not be presented here, as you can look those up in the previous chapter. To summarize: The data were suited for analysis with factor analysis and SEM, but the distribution of the variables is somewhat left-skewed. Therefore, an estimation method that is robust against non-normality should be used.
The one characteristic that needs additional investigation is the sample size. As mentioned in the previous chapter on factor analysis, Bentler and Chou [23] recommend having 5 observations per estimated parameter, while Jackson [24] recommends having 10, and preferably 20 observations, for each parameter you want to estimate. Therefore, the total number of observations depends on the exact model fitted to the data. If you start your SEM analysis with going through all three recommended model-building steps from the previous chapter (see the “Integrated Strategy for Structural Equation Modeling” above), you need to base your required sample size on the number of parameters estimated by an exploratory factor analysis (e.g., for a two-factor model fitted to 10 variables, you would need about (20 factor loadings + 10 intercepts + 10 error-variances) * 10 = 400 cases) and multiply that by 2 to also have enough observations for a new or holdout sample to check generalizability of your factor-model and for fitting your SEM model. Note that the sample size calculated this way is what you need in each relevant subgroup for which you want to assess measurement invariance. As mentioned above, you could go straight to the SEM analysis if you use an existing instrument on a sample from a population for which the instrument has already been validated and shown to be invariant across relevant groups in previous research. In that case, you would need fewer observations because a SEM model (like a CFA model) will have more constraints than an exploratory factor analysis model and hence fewer parameters to estimate.
You will perform the SEM analysis using the holdout sample from the previous chapter. The sample size for that is 438, which is sufficiently large to estimate 20 intercepts, 10 loadings, 10 unique variances, and 10 relations between factors according to the more lenient rules by Bentler and Chou [23]. As you will see in Step 2, this number of parameters aligns well with the SEM model that will be fitted to the data.
5.2 Step 1: Steps from the previous chapter
As explained in the strategy section, it is recommended to go through all the steps mentioned in the previous chapter (exploring the data structure, building the factor model and assessing fit, and assessing generalizability), and the R code for these steps can also be found there. For brevity, the steps and code will not be repeated here. Additionally, configural invariance (tested by following the steps from the previous chapter for each relevant subgroup separately) will be assumed to hold so that this section can focus on the code needed for a SEM analysis. We begin with picking up at the code for randomly assigning 438 rows of the data to a holdout dataset:
set.seed(19)
ind <- sample(c(rep("model.building", 438), rep("holdout", 438)))
tmp <- split(dataset, ind)
model.building <- tmp$model.building
holdout <- tmp$holdoutFor an explanation of the code, please go back to the previous chapter.
5.3 Step 2: Assessing Higher Levels of Invariance
Before looking into the structural relationships of interest, you have to ensure that the loading (and possibly intercept) invariance holds across groups for which this might be violated according to theory. To this end, you first have to specify the model, which is very similar to the model that was specified in the previous chapter for the CFA model. The model syntax looks as follows:
SEM_model <- '
# Regressing items on factors
TSC =~ TSC1 + TSC2 + TSC3 + TSC4 + TSC5
TE =~ TE1 + TE2 + TE3 + TE5
EE =~ EE1 + EE2 + EE3 + EE4
DE =~ DE1 + DE2 + DE3
RPA =~ RPA1 + RPA2 + RPA3 + RPA4
# Relations between factors
TE ~ TSC
EE ~ TE + TSC
DE ~ TE + TSC
RPA ~ TE + TSC
'The first part of this syntax is exactly the same as the syntax that defined the CFA model in the previous chapter, with the syntax elements “=~” indicating that a factor is measured by specific observed variables. The code above defines a model where the factors TSC, TE, EE, DE, and RPA are measured by different sets of variables, which are separated by “+”. In addition to the measurement part, this syntax includes the specification of relations between factors using the “~” operator. For example, TE is regressed onto TSC, indicating a directional relationship from TSC to TE. When comparing this syntax to the one from the previous chapter, you will see that the only thing that changes when you move from CFA to SEM is that you specify concrete structural relations (i.e., which latent factors are regressed on each other) instead of solely specifying correlations. Although intercepts are not explicitly mentioned in the model, they can be included by using the meanstructure = TRUE argument in the command when estimating the model.
Once the model syntax is specified, you can check whether invariance across groups (here, gender) holds. More specifically, you check this by comparing a model with and without equality constraints on the parameters of interest (here, as motivated before, only the loadings) and check whether adding constraints reduces model fit more than desired. To evaluate the degree of fit reduction, you can look at the changes in the global fit measures described in the previous chapter. These were (1) the Chi-squared significance test, (2) the comparative fit index (CFI), (3) the root mean square error of approximation (RMSEA), and (4) the standardized root mean square residual (SRMR). Recall that, unlike the Chi-squared significance test that assesses perfect fit, the CFI, RMSEA, and SRMR assess approximate fit. Similarly, only the Chi-squared significance test is a formal test for assessing invariance. As for assessing global fit, each fit measure is accompanied by rules of thumb when assessing invariance, allowing you to decide whether or not (approximate) invariance holds. The difference is that the rules of thumb now pertain to differences in the criteria between models with and without constraints. The Chi-significance test should be nonsignificant because otherwise, the model with constraints fits significantly worse. Keep in mind, however, that this test easily rejects the assumption of invariance with increasing sample size. Regarding the other three measures, the rules of thumb are that differences in CFI should be smaller than or equal to .01, differences in RMSEA should be smaller than or equal to .015, and differences in SRMR should be smaller than or equal to .030 [25].
You do not have to perform the invariance assessment by constraining parameters yourself. Instead, you can use the command below. The argument model asks you to specify the model syntax, data asks for the dataset that you want to use for the analysis, and group refers to the variable for which you want to assess invariance. The argument estimator indicates which estimation procedure is used. The default is standard maximum likelihood (“ML”) estimation. However, for the current data, a robust maximum likelihood (“MLR”) estimation is applied to account for small violations of the normality assumption. If the data contain missing values, you can add the argument missing and specify it as equal to “fiml”, corresponding to a full information maximum likelihood approach. As already discussed in the previous chapter, this is a sensible approach if you have at least missing at random (MAR) data details about missing data mechanisms can be found in the lavaan tutorial [26]. Next, the argument “intercept” indicates whether intercept invariance should be assessed in addition to loading invariance. If put to TRUE, the output contains information on both loading and intercept invariance unless two or more of the four fit criteria indicate that loading invariance is violated because then, assessing intercept invariance does not make sense. This information would be provided in the form of a message. Finally, the argument “display” indicates whether output about group-specific parameters and differences are provided (when set to TRUE) or not (when set to FALSE).
invarianceCheck(model = SEM_model, data = holdout,
group = "gender", estimator = "MLR", intercept = FALSE,
missing = FALSE, display = FALSE)Nested Model Comparison-------------------------------------------------------------------
Scaled Chi-Squared Difference Test (method = "satorra.bentler.2001")
lavaan NOTE:
The "Chisq" column contains standard test statistics, not the
robust test that should be reported per model. A robust difference
test is a function of two standard (not robust) statistics.
Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
Loadings_Free 320 15711 16283 648.06
Loadings_Invariant 335 15693 16203 660.17 9.8747 15 0.8275
Model Fit Indices ------------------------------------------------------------------------
chisq.scaled df.scaled pvalue.scaled rmsea.robust cfi.robust
Loadings_Free 632.823† 320 .000 .068 .923
Loadings_Invariant 638.987 335 .000 .065† .925†
srmr
Loadings_Free .050†
Loadings_Invariant .053
Differences in Fit Indices ---------------------------------------------------------------
df.scaled rmsea.robust cfi.robust srmr
Loadings_Invariant - Loadings_Free 15 -0.002 0.002 0.002
Loading Invariance Interpretation --------------------------------------------------------
The hypothesis of perfect loading invariance *is not* rejected according to the
Chi-Square difference test statistics because the p-value is larger or equal to 0.05.
The hypothesis of approximate loading invariance *is not* rejected
according to the CFI because the difference in CFI value is smaller than
or equal to 0.01.
The hypothesis of approximate loading invariance *is not* rejected
according to the RMSEA because the difference in RMSEA value is smaller
than or equal to 0.015.
The hypothesis of approximate loading invariance *is not* rejected
according to the SRMR because the difference in SRMR value is smaller than
or equal to 0.030.
Inspecting the output, you can see several sections. You may directly go to the last section “Loading Invariance Interpretation” because this provides you with information on whether or not invariance is rejected according to the four fit measures (following the cut-off values provided before). If you are interested in (reporting) details about the Chi-square significance test and the (differences in) model fit criteria, you can also inspect the beginning of the output.3 It can be seen that invariance is not rejected according to any of the criteria. Similar to assessing model fit in factor analysis, it is advised that no more than one criterion should reject invariance for concluding that invariance holds. If this is initially not the case, you may release one equality constraint at a time (i.e., moving towards partially invariant models) and run the invarianceCheck() function again until partial invariance holds. In order to decide which constraints to release, you can consult the information provided when the “display” argument is set to TRUE. The output will then show the loadings and intercepts per group as well as the differences in these parameters across groups. You will also get a message indicating which loading (and intercept) differs most between groups. These would be the first targets to estimate freely across groups (while making sure that the minimum requirements for partial invariance mentioned above hold). How to update the model syntax to freely estimate parameters between groups is explained on the lavaan package website [26].
5.4 Step 3: Building the Structural Equation Model and Assessing Fit
The next step is to perform the SEM analysis on the holdout data using the specified SEM model with the following command:
sem_robust <- sem(model = SEM_model, data = holdout, std.lv = TRUE,
estimator = "MLR", meanstructure = TRUE)The arguments are the same as for the cfa() function discussed in the previous chapter. The relevant (standardized) output about the structural relations can be extracted from the SEM model with the command below. The first argument asks you to specify the lavaan object from which you want to extract the structural relations, nd lets you specify the number of decimals you want to display (with default 3).
sem_structural_results(sem_robust, nd = 3) outcome predictor std estimate se p-value
1 TSC TE 0.693 0.121 0
2 TSC EE 0.547 0.17 0
3 TSC DE 0.4 0.143 0
4 TSC RPA 0.413 0.111 0
5 TE EE 0.32 0.114 0
6 TE DE 0.293 0.088 0.001
7 TE RPA 0.326 0.084 0Looking at the output from left to right, you can see the outcome variable of the structural relationship, the predictor of the structural relationship, the regression coefficient, the standard error of the regression coefficient, and the p-value of the effect. Here, you see that all structural relations are significantly different from zero and thus that TE, EE, DE, and RPA are all related to TSC and that EE, DE, and RPA are related to TE. As mentioned, the function sem_structural_results() displays the most relevant information about the structural relations. For more information and unstandardized estimates, you can use the summary() function on the lavaan object sem_robust also see the lavaan tutorial by [27].
6 Conclusion
SEM is a rich, powerful, and mature statistical framework that has more than a century of evolution and expansion. Several other extensions have been developed to include dynamic structural equation modelling for the analysis of temporal data, latent growth curve modelling for the analysis of systematic change over time, and multilevel SEM for the analysis of hierarchically clustered (or nested) data, to mention just a few. This chapter merely provided a primer that introduces the basics of the methods and an example application. Hopefully, it opens the door for interested readers to explore such a powerful framework that offers an excellent solution to many of the analytical tasks that researchers seek.
7 Further readings
In this chapter, you have seen an introduction and tutorial on how to apply SEM in educational research. To learn more about how SEM can be applied to this field, you can consult these resources:
Teo, T., Ting Tsai, L., & Yang, C. 2013. "Applying Structural Equation Modeling (SEM) in Educational Research: An Introduction". In Application of Structural Equation Modeling in Educational Research and Practice.
Khine, M. S., ed. 2013. “Application of Structural Equation Modeling in Educational Research and Practice”. Contemporary Approaches to Research in Learning Innovations.
To learn more about SEM in general, you can refer to the following:
Kline, R. B. 2015. “Principles and Practice of Structural Equation Modeling”. 4th Edition. Guilford Publications.
Hoyle, Rick H. 2012. “Handbook of Structural Equation Modeling”. Guilford Press.
References
1.
Vogelsmeier LVDE, Saqr M, López-Pernas S, Jongerling J (2024) Factor analysis in education research using r. In: Saqr M, López-Pernas S (eds) Learning analytics methods and tutorials: A practical guide using r. Springer, pp in–press
2.
Teo T, Tsai LT, Yang C-C (2013) Applying structural equation modeling (SEM) in educational research: An introduction. In: Application of structural equation modeling in educational research and practice. Brill, pp 1–21
3.
Wright S (1921) Correlation and causation. Journal of Agricultural Research 20:557–585
4.
Jöreskog KG, Van Thillo M (1972) LISREL: A general computer program for estimating a linear structural equation system involving multiple indicators of unmeasured. ETS Research Bulletin Series
5.
Davis FD (1993) User acceptance of information technology: System characteristics, user perceptions and behavioral impacts. International journal of man-machine studies 38:475–487
6.
Valtonen T, López-Pernas S, Saqr M, Vartiainen H, Sointu ET, Tedre M (2022) The nature and building blocks of educational technology research. Computers in human behavior 128:107123
7.
Cardona Valencia D, Betancur Duque FA (2023) Technology acceptance model (TAM): A study of teachers’ perception of the use of serious games in the higher education. IEEE Revista Iberoamericana de Tecnologias del Aprendizaje 18:123–129
8.
Abd Majid F, Mohd Shamsudin N (2019) Identifying factors affecting acceptance of virtual reality in classrooms based on technology acceptance model (TAM). Asian journal of university education 15:51
9.
Nja CO, Idiege KJ, Uwe UE, Meremikwu AN, Ekon EE, Erim CM, Ukah JU, Eyo EO, Anari MI, Cornelius-Ukpepi BU (2023) Adoption of artificial intelligence in science teaching: From the vantage point of the african science teachers. Smart learning environments 10: https://doi.org/10.1186/s40561-023-00261-x
10.
Marangunić N, Granić A (2015) Technology acceptance model: A literature review from 1986 to 2013. Universal access in the information society 14:81–95
11.
Kusurkar RA, Ten Cate TJ, Vos CMP, Westers P, Croiset G (2013) How motivation affects academic performance: A structural equation modelling analysis. Advances in health sciences education: theory and practice 18:57–69
12.
Kucuk S, Richardson JC (2019) A structural equation model of predictors of online learners’ engagement and satisfaction. Online Learning 23:196–216
13.
Araka E, Maina E, Gitonga R, Oboko R (2020) Research trends in measurement and intervention tools for self-regulated learning for e-learning environments—systematic review (2008–2018). Research and practice in technology enhanced learning 15: https://doi.org/10.1186/s41039-020-00129-5
14.
Koç M (2017) Learning analytics of student participation and achievement in online distance education: A structural equation modeling. Educational Sciences: Theory & Practice 17: https://doi.org/10.12738/estp.2017.6.0059
15.
Fincham E, Whitelock-Wainwright A, Kovanović V, Joksimović S, Staalduinen J-P van, Gašević D (2019) Counting clicks is not enough: Validating a theorized model of engagement in learning analytics. In: Proceedings of the 9th international conference on learning analytics & knowledge. Association for Computing Machinery, New York, NY, USA, pp 501–510
16.
Jöreskog KG (1971) Simultaneous factor analysis in several populations. Psychometrika 36:409–426
17.
Sörbom D (1974) A general method for studying differences in factor means and factor structure between groups. The British journal of mathematical and statistical psychology 27:229–239
18.
Bauer DJ, Hussong AM (2009) Psychometric approaches for developing commensurate measures across independent studies: Traditional and new models. Psychological methods 14:101–125
19.
Byrne BM, Shavelson RJ, Muthén B (1989) Testing for the equivalence of factor covariance and mean structures: The issue of partial measurement invariance. Psychological bulletin 105:456–466
20.
Steenkamp J-BEM, Baumgartner H (1998) Assessing measurement invariance in cross‐national consumer research. The journal of consumer research 25:78–107
21.
Prasojo LD, Habibi A, Mohd Yaakob MF, Pratama R, Yusof MR, Mukminin A, Suyanto, Hanum F (2020) Teachers’ burnout: A SEM analysis in an asian context. Heliyon 6:e03144
22.
López-Pernas S, Saqr M, Conde J, Del-Rı́o-Carazo L (2024) A broad collection of datasets for educational research training and application. In: Saqr M, López-Pernas S (eds) Learning analytics methods and tutorials: A practical guide using R. Springer, pp in–press
23.
Bentler PM, Chou C-P (1987) Practical issues in structural modeling. Sociological methods & research 16:78–117
24.
Jackson DL (2003) Revisiting sample size and number of parameter estimates: Some support for the n:q hypothesis. Structural equation modeling: a multidisciplinary journal 10:128–141
25.
Chen FF (2007) Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural equation modeling: a multidisciplinary journal 14:464–504
26.
Rosseel Y (2012) Lavaan: An r package for structural equation modeling. Journal of statistical software 48: https://doi.org/10.18637/jss.v048.i02
27.
Rosseel Y (2023) The lavaan tutorial
Note that observed variables (such as age or gender) can just be added to your SEM model. Only multiple-item instruments to assess psychological constructs must be validated. Thus, you can ignore the observed variables in this first SEM step.↩︎
We contacted the authors, but they refrained from sharing the variable because they still plan to conduct research using the variable.↩︎
Note that you will first see a note from lavaan about ‘the "Chisq" column contain[ing] standard test statistics’. You can simply ignore this, as it just gives information on how the difference in fit was tested.↩︎